SQLITE NOT INSTALLED
Декартовы координаты, известные также как прямоугольные координаты, являются одним из наиболее популярных методов описания положения в пространстве. Они были впервые введены французским математиком и философом Рене Декартом в XVII веке. Декартовы координаты стали основой для развития аналитической геометрии и являются неотъемлемой частью современной математики и физики.
Что представляют собой Декартовы координаты?
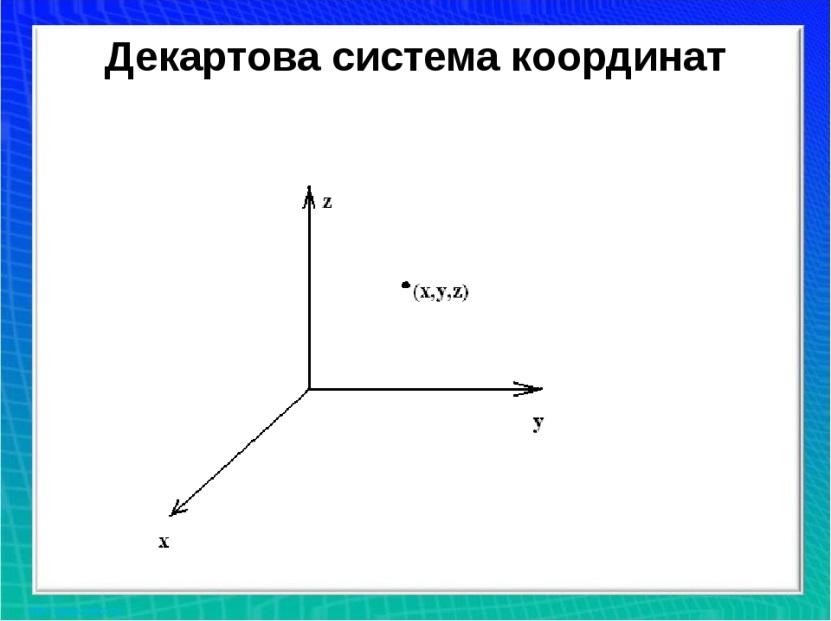
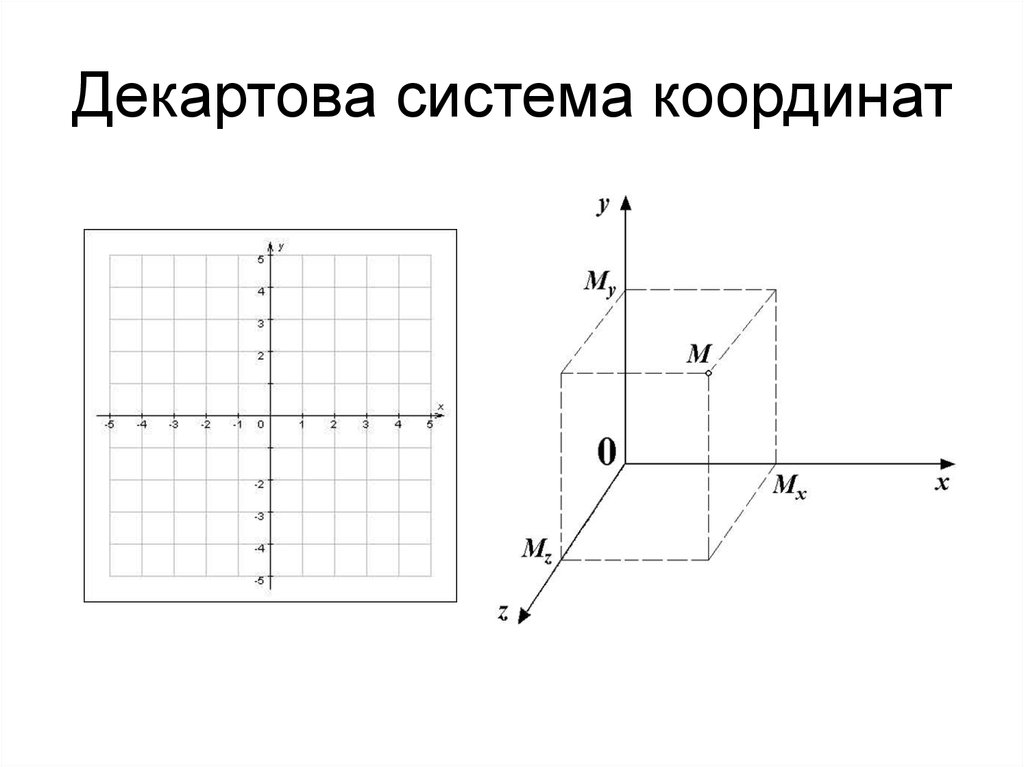
Декартовы координаты состоят из двух или трех чисел, обозначающих положение точки в пространстве. При двумерных координатах эти числа представляют собой упорядоченную пару (x, y), где x — это координата точки на горизонтальной оси (ось абсцисс), а y — на вертикальной оси (ось ординат). В трехмерном случае используется упорядоченная тройка (x, y, z), где z — это координата точки на оси глубины (ось аппликат).
Декартовы координаты позволяют однозначно идентифицировать любую точку в пространстве. Координаты определенной точки могут быть положительными, отрицательными или нулевыми, в зависимости от ее положения относительно начала координат. Начало координат обозначается обычно буквой O и считается точкой с нулевыми координатами (0, 0) или (0, 0, 0).
Преимущества использования Декартовых координат
Декартовы координаты имеют множество преимуществ, что делает их широко используемыми в различных областях науки и техники:
- Простота в использовании: Описание положения точки в виде чисел позволяет легко выполнять различные операции, такие как сложение, вычитание, умножение и деление. Это делает Декартовы координаты удобными для решения математических задач.
- Универсальность: Декартовы координаты можно использовать для описания положения в двумерном и трехмерном пространстве. Они применимы в геометрии, физике, компьютерной графике, навигации и других областях.
- Геометрическая интерпретация: Декартовы координаты позволяют геометрически интерпретировать математические операции. Например, сложение векторов может быть представлено как перемещение точки из одного места в другое.
Пример использования Декартовых координат
Рассмотрим пример применения Декартовых координат в геометрии. Предположим, у нас есть две точки A и B с координатами A(x1, y1) и B(x2, y2). Чтобы найти расстояние между этими точками, мы можем использовать формулу расстояния между двумя точками в Декартовой системе координат:
d = √((x2 - x1)2 + (y2 - y1)2)
Эта формула основана на теореме Пифагора, где d — это расстояние между точками A и B. Мы вычитаем координаты x и y каждой точки и возводим результаты в квадраты. Затем мы суммируем квадраты и берем квадратный корень от суммы для получения окончательного значения расстояния.
Вывод
Декартовы координаты являются мощным инструментом для описания положения в пространстве. Они предоставляют удобный и понятный способ записи и визуализации точек. Благодаря своей универсальности и геометрической интерпретации, Декартовы координаты находят широкое применение в науке и технике.